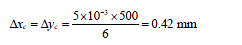由式(3)可知位置误差与速度误差相关,速度误差与2 个加速度计误差和1 个陀螺仪误差都相关,精确分析较困难,对其进行近似分析。本文中AGV 的满载速度为3 m/s,加速度为0.3 m/s2。目前,中等陀螺仪的偏差是20°/ h ,中等加速度计的偏差是10-2g,有
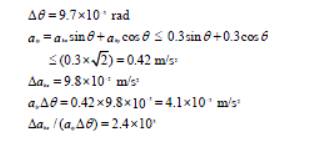
由于Δabx 远大于aiyΔθ,Δvix 的主项为Δabxcosθ-Δabysinθ,aiyΔθ 可忽略不计,则简化误差方程为
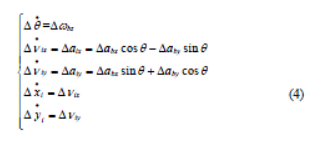
为不失一般性,设Δabx=Δaby,式(4)简化为
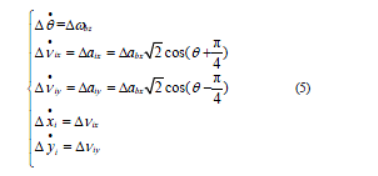
对式(5)中加速度误差进行两次积分,得到位置误差方程
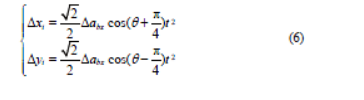
式(6)中,t 为ArUco 标签的数据更新时间。基于视觉ArUco 标签技术的AGV 组合导航系统定位精度由3 个因素决定: 加速度计偏差Δabx、AGV 运行方向θ和ArUco 标签数据更新时间t。
AGV 的定位精度随ArUco 标签数据更新时间t 的增大而增大,当AGV 检测到下一个ArUco 标签时,定位误差恢复到基于视觉的ArUco 标签定位误差, ArUco标签间距越短,AGV 组合导航系统的更新时间越短,AGV 的定位精度越高。
铁路物流园堆场内AGV 转运集装箱沿着xi 轴方向满载启动行驶,运行100 m 才能检测到下一个ArUco标签,运行时间为38.3 s,加速计的精度为4×10-3g。将上述数据代入式(6)得
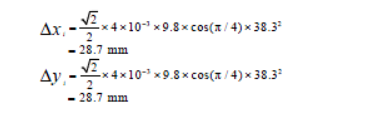
AGV 空载以6 m/s 的速度恒速运行时位置误差为

AGV 距离ArUco 标签3 m 时可检测识别出前摄像头可视区的ArUco 标签,根据相机内参数、ArUco 标签的特征点、相机成像模型计算AGV 与ArUco 标签之间的相对位置关系,ArUco 标签的经纬度已知,经过坐标转换得出AGV 的经纬度。针孔相机模型见图2。
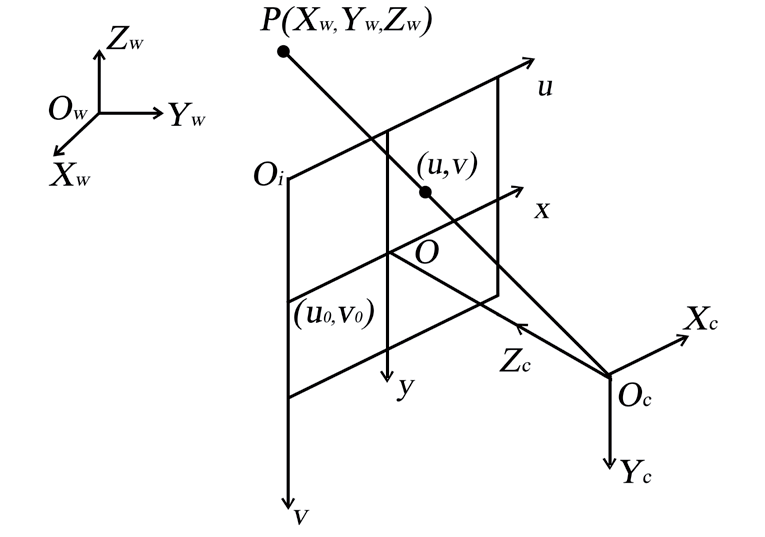
图2 针孔相机模型
如图2 所示,Ow-Xw Yw Zw 为世界坐标系,Oc-Xc YcZc为摄像机坐标系,O-xy 为图像物理坐标系,Oi-uv 为图像像素坐标系, Oc 为摄像机的光学中心,Oc 在图像平面的投影点坐标为(u0,v0),Oc 到图像平面的距离为焦距f,点P 在世界坐标系的坐标为(Xw ,Yw ,Zw),点P 在图像像素坐标系的坐标为(u,v),根据透视投影几何关系点P 在图像物理坐标系的坐标为[6]
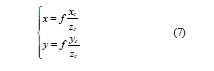
将点P 在图像物理坐标系的坐标转换为图像像素坐标系坐标,并用齐次坐标与矩阵表示为[6]
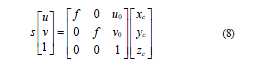
世界坐标系在摄像机坐标系的姿态和位置可以用旋转矩阵和平移向量来描述,则点在世界坐标系的坐标和摄像机坐标系的坐标转换为[6]
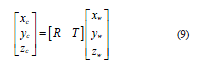
将式(9)代入式(8)中,得到空间点的图像坐标与实际三维坐标之间的关系为[6]
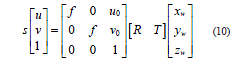
式(10)中,使用相机标定获取相机内参数(f,u0 ,v0 ),AGV 前摄像头检测出ArUco 标签后,根据ArUco 标签特征点在世界坐标系的实际三维坐标和对应特征点在图像像素坐标系的坐标,可以求出旋转矩阵R 和平移向量T,即AGV 前摄像头与ArUco 标签的位姿关系。相机标定内参数有一定误差和相机镜头存在畸变等因素影响摄像头测量精度,测量X 轴方向AGV 前摄像头与ArUco标签不同距离时的摄像头的测量误差如图3 所示,AGV前摄像头检测到ArUco 标签时的误差小于15 mm。
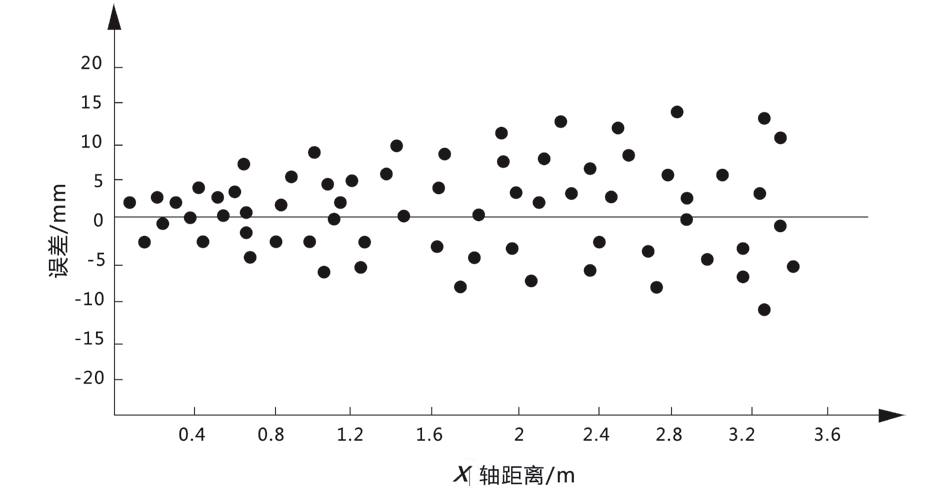
图3 X 轴方向偏差
AGV 转运集装箱,沿着xi 轴方向满载启动行驶,运行100 m 到检测到下一个ArUco 标签进行惯性导航系统数据更新时定位误差变换为AGV 前摄像头定位误差,如图3 所示,随着AGV 前摄像头接近ArUco 标签,前摄像头定位误差小于5 mm,即最终惯性导航系统数据更新后定位误差小于5 mm。由惯性导航系统误差累积特性得到AGV 粗定位最大误差为
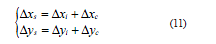
式中: Δxs 是AGV 在xi 轴的最大位置误差,Δys 是AGV 在yi 轴的最大位置误差,Δxi 是惯性导航系统xi 轴最大位置误差,Δyi 是惯性导航系统yi 轴最大位置误差,Δxc 是前摄像头xi 轴最小位置误差,Δyc 是前摄像头yi轴最小位置误差。
由式(11)得出AGV 在运动过程中轴理论定位误差是33.7 mm,通过多次实际测量取平均值得到AGV在x 轴的定位误差45 mm,与定位误差理论计算值比较接近。
2.2 AGV 精确定位系统精度
使用AGV 俯视摄像头检测备位标签,通过提取备位标签角点特征,得到备位标签在图像像素坐标系的坐标(x,y),由相机成像模型,测量AGV 与备位标签之间的实际距离,实现AGV 装卸集装箱时的精确定位导航。由式(7)得出点P 在相机坐标系的坐标为
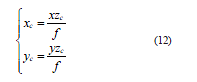
AGV 俯视摄像头与地面相对位置固定,即zc 为一定值,对式(12)变分得位置误差方程
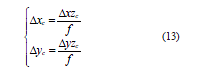
备位标签在图像像素坐标系的最小距离变化量为单个像素,本文中,俯视摄像头像素长宽尺寸各为5um,焦距f = 6 mm,俯视摄像头离地500 mm,将上述参数代入式(13),得出位置误差